Information loss paradox
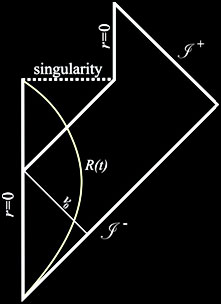
Image: Penrose diagram for an evaporating black hole
According to classical general relativity, nothing can escape from a black hole – but plenty can fall into it, quite apart from the original stellar collapse by which it was formed. The no-hair theorem proved in the 1960s shows that despite the vast amount of information (or structure) of the matter thus absorbed, exactly three parameters characterize the black hole: its mass, charge, and angular momentum. But the ‘missing information’ can be imagined still to be contained within the black hole, as on classical principles black holes are indestructible: they can only grow.
However, according to Hawking’s influential arguments of 1975, black holes of mass M emit a thermal spectrum of radiation characteristic of black bodies at temperature
T= hc3/4GMk, where G is the gravitational constant, h is Planck’s constant, and k is Boltzmann’s constant. When M is measured in kg and T in Kelvins (SI units), T=1.227x1023/M. This temperature is therefore negligible for black holes formed by stellar collapse (of a few solar masses, about 1031 kg), but over sufficiently long periods of time – vastly greater than the lifetime of the universe to date – the temperature of the cosmic microwave background will fall below black hole temperatures, and, since eventually there will be no further accretion of matter, net energy will be radiated away, and black hole masses will start to fall. It is a process that accelerates over time: eventually, when the mass is small, a black hole will emit a thermal spectrum of intense gamma rays, leptons, and mesons, at a temperature not seen in the universe since reheating following the inflationary expansion and the primordial fireball of the big bang. The culmination is a black hole explosion: whether there is a remnant ‘naked’ singularity is unknown, but otherwise there is only thermalized energy dumped back into the void – energy that by definition contains no information. What has happened to all the structure – hence information – lost to the black hole when it was formed, and subsequently? This is the information loss paradox. It is a paradox because it is assumed that all fundamental dynamical processes are time-symmetric – in particular, in quantum theory, that the dynamics is unitary. Information can never be lost by such processes.
Hawking’s theory of black-hole radiation was also developed by Jacob Bekenstein; it has come to be known as black hole thermodynamics. The existence of Hawking radiation is now widely accepted, and the information-loss paradox thus only strengthened. However the holographic principle, first proposed by Gerard t’Hooft in 1993 and extended to superstring theory by Leonard Susskind, offers a potential solution. So too does the AdS/CFT correspondence first discovered by Juan Maldaceni in 1997, which not only gives support to the holographic principle but in establishing an equivalence between gravitational (superstring or M theory) physics and quantum field theories involving non-gravitational physics appears to imply that gravity cannot really be in conflict with the unitary formalism of quantum theory.
Hawking himself arrived at another solution to the paradox (which may of course explain how Maldaceni-type duality theorems are possible). In a paper published in 2004 he argued that quantum perturbations at the black hole event horizon modified the radiation emitted so that it was not purely thermal, allowing information to escape. But others, notably Roger Penrose, embrace the ‘paradox’, arguing that we should expect information loss – the loss of unitarity and the emergence of irreversible physics – just when gravitational effects become relevant to quantum lengthscales. According to Penrose, as to many others, a solution to the measurement problem in quantum mechanics requires objective wave-packet collapse, contrary to the many-worlds interpretation as developed by Everett and the pilot wave theory developed by de Broglie and Bohm.
Links
Scholarpedia: Black hole entropy >
Scholarpedia: Hawking radiation >
Wikipedia: The information loss paradox >
Wikipedia: The holographic principle >
Hawking’s change of mind: report from Nature >
Jacob Bekenstein in Scientific American >
Multimedia
Leonard Susskind: the world as hologram >
Raphael Buosso: the world as a hologram >
BBC Horizon: the Hawking paradox >

