The AdS/CFT correspondence
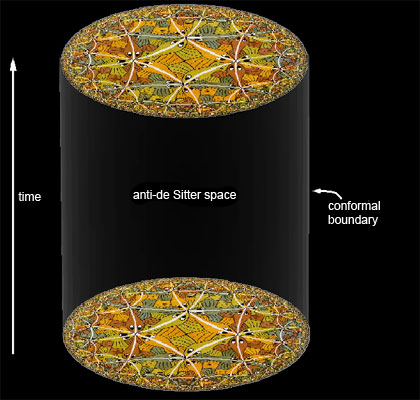
Image: a representation of an anti-de Sitter space in d=2+1 dimensions. Each 2-dimensional section is a hyperbolic space, the straight lines of which are represented as curved lines in Escher’s woodcut ‘Circle Limit III’. The boundary to this space is d-1 dimensional (2 dimensional); symmetries that preserve the metric of anti-de Sitter space act as conformal transformations on the boundary.
Source: Wikipedia commons
String theory in D=10 dimensions, or M theory in D=11 dimensions, is usually thought to recover 4-dimensional spacetime through compactification , the ‘curling-up’ of the extra dimensions, in 6 or 7-dimension manifolds MD-4. The enormously large number of ways that this can be done has been estimated as of order 10500. Each different compatification has a different vacuum state, leading to essentially distinct theories.
However, an entirely new way of thinking about the string and M theory description of 4 dimensional space-time was opened by Juan Maldacena in 1998, specifically when the non-compactified dimensions take the form of anti-de Sitter spacetime AdSd, the homogeneous and isotropic solution to the source-free Einstein field equations with negative cosmological constant, in d dimensions. Spatial sections of this space are hyperbolic spaces -- spaces of constant negative curvature -- as first discovered by the Hungarian mathematician János Bolyai and, independently, the Russian mathematician Nokolai Lobachevski, in 1830-31. In an AdSd space, the isometries of the metric (transformations that leave the metric structure invariant) act as the conformal group on the d-1 dimensional boundary. It is this fact that underlay Maldacena’s construction. He showed that a superstring or M theory on the background AdSd x MD-d is equivalent – or ‘dual’ – to an ordinary but conformally invariant quantum field theory on a flat d-1 dimensional Minkowski space.
Such a duality, according to which every physical quantity definable in the one theory has an analogue in the other, is similar to the holographic principle introduced by Gerard t’Hooft. The terminology draws on the sense in which information about three-dimensional objects can be encoded in a two-dimensional surface (a hologram). Maldacena’s work was almost immediately extended by Gubser, Klebanov, and Polyakov in 1998, and by Witten in a paper that same year, to show that a type IIB string theory on AdS5 x S5 (where S5 is the 5-dimensional sphere) is dual to N=4 super-symmetric Yang-Mills theory on 4-dimensional Minkowski spacetime. The latter theory, despite the fact that it has unbroken super-symmetry, has similarities to QCD. Subsequently many other examples of the duality have been discovered. Whether they are only calculational devices, or indicate a deeper connection between gravity as an emergent structure of a conformal quantum field theory, remains unknown. However, insofar as a form of Maldacena duality extends to black hole thermodynamics – and there are indications that it does -- the AdS/CFT correspondence surely has a bearing on the information-loss paradox.
As of 2010 Maldacena’s paper of 1998 was the most highly cited paper in high energy physics with over 7000 citations.
Links
Jens Lyng Petersen, ‘Introduction to the Maldacena conjecture on AdS/CFT >
Wikipedia: The AdS/CFT correspondence >
Wikipedia: The holographic principle >
Multimedia
Physics@FOM Veldhoven 2012, Juan Maldacena, Master class 1 >
Physics@FOM Veldhoven 2012, Juan Maldacena, Master class 2 >
Juan Maldacena: Black holes and the structure of spacetime >

