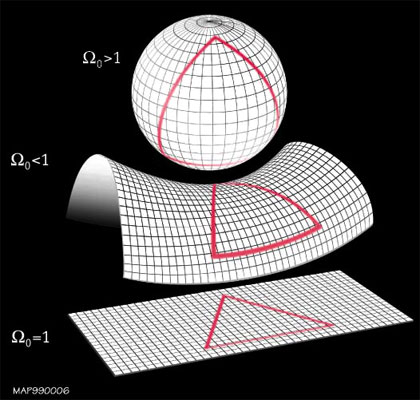
Flatness Problem
Image: According to General Relativity, curvature is dynamical: what then dictates its almost exact flatness in the early universe?
The flatness problem is an example of fine-tuning, noticed by Dicke in 1969. In Friedmann's equation the expansion of the universe is controlled by two factors: the total energy density and the curvature. Today we find from supernova observations that these two numbers cancel almost exactly, yielding a universe which is very close to being flat. When extrapolated backwards the difference between these two numbers shrinks down rapidly, with there difference being less than one part in 10^62.
Proposed solutions to the flatness problem include anthropic reasoning – that we could not observe a universe which was not close to being flat as galaxies would not persist long enough for life to evolve, and cosmic inflation.
Links
Ned Wright on the nature of curvature >
Cormac O’Rafferty : the flatness problem >
Wikipedia: the flatness problem >

